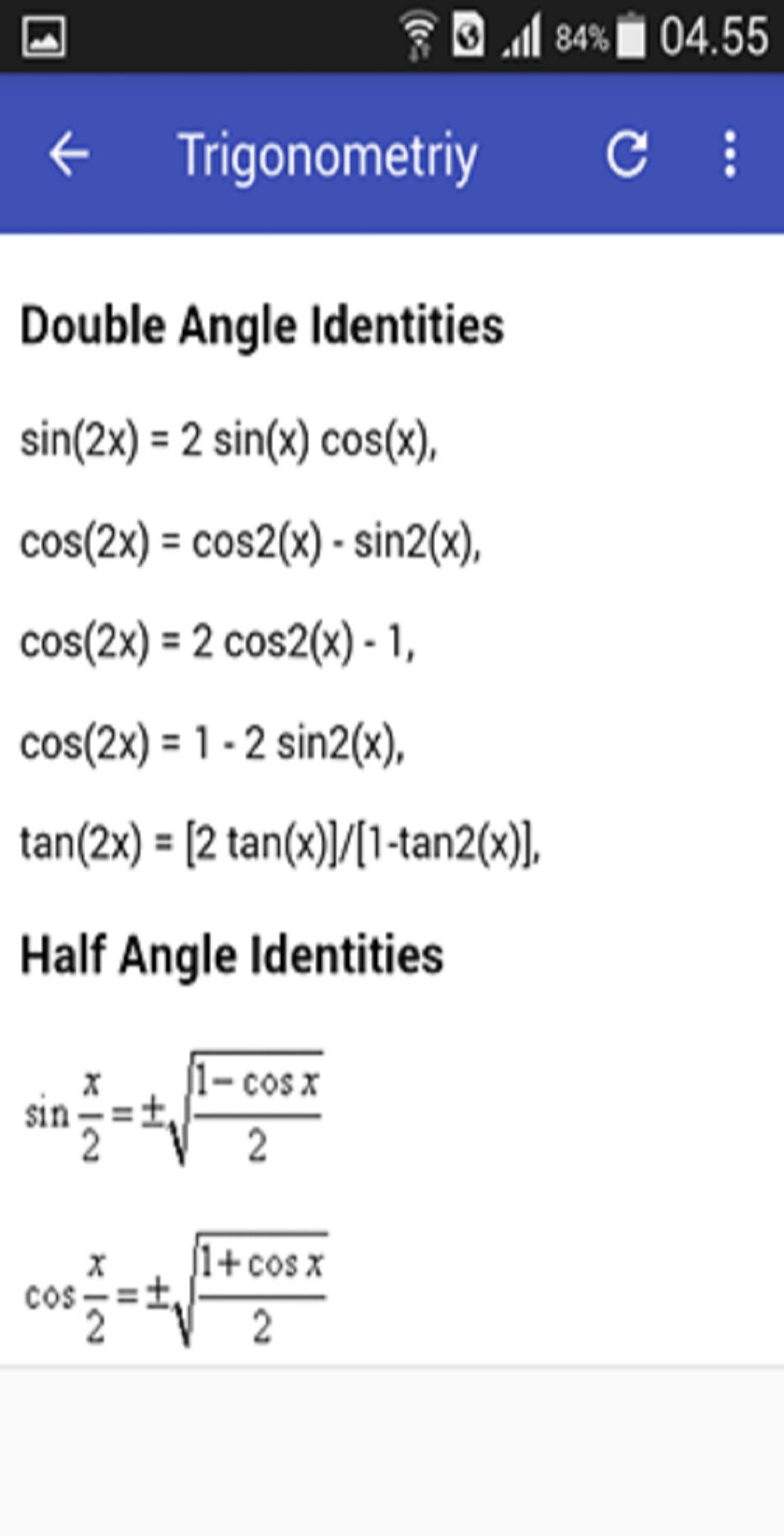
The trigonometric formulas like Sin2x, Cos 2x, Tan 2x are popular as double angle formulae, because they have double angles in their trigonometric functions For solving many problems we may use these widely The Sin 2x formula is Where x is the angle General solution of tan(2x)tan(x) = 1 For the question, tan(2x)tanx = 1, I divided it by tanx, and got the solution as ( 2n 1) π 6 tan2x = cotx = tan(π 2 − x) So, 2x = nπ π 2 − x So, 3x = ( 2n 1) π 2 But the book solved using the formula of tan(2x), and got the solution as ( 6n ± 1) π 6 I can see that my solution has odd= 1 – 2 sin2 x = 2 cos2 x – 1 • Tangent tan 2x = 2 tan x/1 tan2 x = 2 cot x/ cot2 x 1 = 2/cot x – tan x tangent doubleangle identity can be accomplished by applying the same methods, instead use the sum identity for tangent, first • Note sin 2x ≠ 2 sin x;

Tan 2x Formula What Is Tan 2x Formula Examples
Tan 2x formula in terms of cos
Tan 2x formula in terms of cos-Verify cos x (cos x/ (1 – tan x)) = (sin x cox x)/ (sin x – cos x) 355 Integral of (e^2x 1)/ (e^2x 1) 405 tan (A B) tan (x y) tan (A B) tan (x y) 250 Switch cameraYou could take tan(x) out of the fraction, but I still don't know how to go about simplifying it The book says the answer is




Exam December 13 Questions Studocu
About Press Copyright Contact us Creators Advertise Developers Terms Privacy Policy & Safety How works Test new features Press Copyright Contact us CreatorsTan 2x ≠ 2 tan x by Shavana Gonzalez Homework Statement cosx=12/13 3pi/2 is less than or equal to x is less than or equal to 2pi Homework Equations sin2x = 2sinxcosx cos2x = 12(sinx)^2 tan2x = (2tanx)/(1(tanx)^2) The Attempt at a Solution Using the tan2x formula, I get 60/47 Using
Expand tan (4x) tan (4x) tan ( 4 x) Factor 2 2 out of 4x 4 x tan(2(2x)) tan ( 2 ( 2 x)) Simplify the numerator Tap for more steps Apply the tangent double angle identity 2 2 tan ( x) 1 − tan 2 ( x) 1 − tan 2 ( 2 x) 2 2 tan ( x) 1 tan 2 ( x) 1 tan 2 ( 2 x) Simplify the denominatorThis is very easy, and this involves the use of trig identities math\displaystyle \int \tan ^2\left(x\right)\,dx/math Since math\tan ^2\left(x\right)=1\sec ^2\left(x\right)/math, so we rewrite the equation as mathFormulas and identities of sin 2x, cos 2x, tan 2x, cot 2x, sec 2x and cosec 2x are known as double angle formulas because they have angle double of the angle present in their formulas Sin 2x Formula Sin 2x formula is 2sinxcosx Image will be uploaded soon Sin 2x =2 sinx cosx Derivation of Sin2x Formula
32 Solve tan 2 x = 0 Setting any of the variables to zero solves the equation t = 0 a = 0 n = 0 x = 0 Solving a Single Variable Equation 33 Solve n1 = 0 Add 1 to both sides of the equation n = 1 Parabola, Finding the Vertex 34 Find the Vertex of y = n 2 n1Tan(2x) is a doubleangle trigonometric identity which takes the form of the ratio of sin(2x) to cos(2x) sin(2 x ) = 2 sin( x ) cos( x ) cos(2 x ) = (cos( x ))^2 – (sin( xFirst, notice that the formula for the sine of the halfangle involves not sine, but cosine of the full angle So we must first find the value of cos(A) To do this we use the Pythagorean identity sin 2 (A) cos 2 (A) = 1 In this case, we find cos 2 (A) = 1 − sin 2 (A) = 1 − (3/5) 2 = 1 − (9/25) = 16/25 The cosine itself will be plus



Solved Givencos 3 0 5 Findtan2 6 Use The Formulatan2x 1 Cos2x 1 Cos2x Course Hero




Limit X Tends 0 X 2 Tan2x Tanx Brainly In
Formulas expressing trigonometric functions of an angle 2x in terms of functions of an angle x, sin(2x) = 2sinxcosx (1) cos(2x) = cos^2xsin^2x (2) = 2cos^2x1 (3) = 12sin^2x (4) tan(2x) = (2tanx)/(1tan^2x)Problem Set 53 Double Angle, Half Angle, and Reduction Formulas 1 Explain how to determine the reduction identities from the doubleangle identity cos(2x) = cos2x−sin2x cos ( 2 x) = cos 2 x − sin 2 x 2 Explain how to determine the doubleangle formula for tan(2x) tan ( 2 x) using the doubleangle formulas for cos(2x) cos Double Angle Formulas The trigonometric double angle formulas give a relationship between the basic trigonometric functions applied to twice an angle in terms of trigonometric functions of the angle itself Tips for remembering the following formulas We can substitute the values ( 2 x) (2x) (2x) into the sum formulas for sin \sin sin and




If Sin X 1 5 And X Is In Quadrant I Find The Exact Values Of The Expressions Without Solving For X Wyzant Ask An Expert




1700tutorial 1 Lab 1 Calc Studocu
Yes, there is We know that mathcos 2x = cos^2 x sin^2 x/math As mathcos^2 x sin^2 x = 1/math, we can write, mathcos 2x = 1 sin^2 x sin^2 x = 1 2 sin^2 x/math or math1 cos 2x = 2 sin^2 x/math Cheers!!!Integral of tan^2x, solution playlist page http//wwwblackpenredpencom/math/Calculushtmltrig integrals, trigonometric integrals, integral of sin(x), integTan2x Formulas Tan2x Formula = 2 tan x 1 − t a n 2 x We know that tan (x) = sin (x)/cos (x) Then, tan2x formula = sin (2x)/cos (2x) Tan 2x can also be written in terms of sin x and cos x, Tan2x Formula in terms of cos x = 2 s i n ( x) c o s ( x) c o s 2 x − s i n 2 x




Tanx Tan2x Tan3x 0



2
Introduction to Tan double angle formula let's look at trigonometric formulae also called as the double angle formulae having double angles Derive Double Angle Formulae for Tan 2 Theta \(Tan 2x =\frac{2tan x}{1tan^{2}x} \) let's recall the addition formula \(tan(ab) =\frac{ tan a tan b }{1 tan a tanb}\) So, for this let a = b , it becomesHouston Texans Nike Shorts Men's Navy DriFit Used Multiple Sizes $3399 Was $3999 Free shipping Benefits charity Nike Men's Dr•Fit Deshaun Watson Houston Texans 🏈 Battle Red Jersey Sz XL NEW $99 Was $ = cos 2 x – 1 cos 2 x = 2cos 2 x – 1 For tan 2x Next Triple angle formulas→ Chapter 3 Class 11 Trigonometric Functions (Term 2) Concept wise;




Find Sin 2x Cos 2x And Tan 2x If Tan X 3 And X Gauthmath
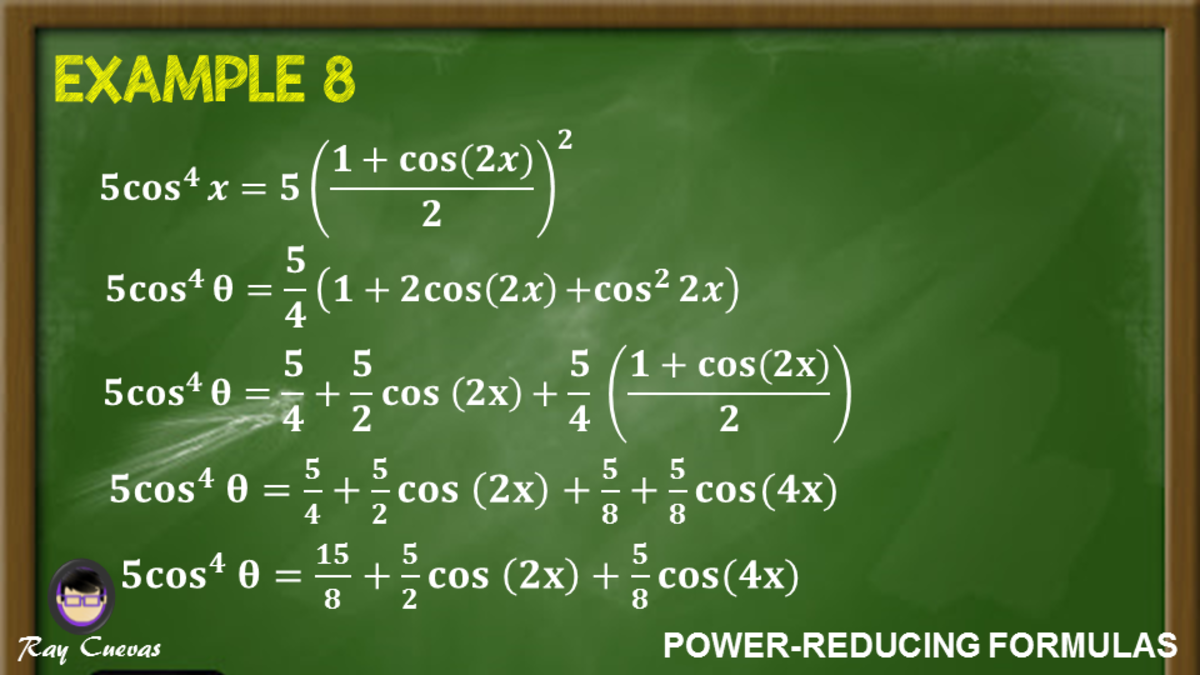



Power Reducing Formulas And How To Use Them With Examples Owlcation
Explanation Change to sines and cosines then simplify 1 tan2x = 1 sin2x cos2x = cos2x sin2x cos2xSolution Using Trigonometric identities Cos 2 x = 1 Sin 2 x Cos 2 x = 1 – (4/5) 2 = 1 – 16/25Proof Half Angle Formula tan (x/2) Product to Sum Formula 1 Product to Sum Formula 2 Sum to Product Formula 1 Sum to Product Formula 2 Write sin (2x)cos3x as a Sum Write cos4xcos6x as a Product Prove cos^4 (x)sin^4 (x)=cos2x Prove sinxsin (5x)/ cosxcos (5x)=tan3x




Lesson 4 5 Double Angle Formulas



Q Tbn And9gcsxz Hkczzvj4wy3gx0dbnqphk3hi Cp Rmi Vgbp2veivzqwuc Usqp Cau
Sin 2x sin(2x) Identity for sin 2x Formula for sin 2x Prove That sin(2x)=2tanx/(1 tan^2x)#sin, #sine, #sine of 2x, #sin 2x, #trigonometryProportionality constants are written within the image sin θ, cos θ, tan θ, where θ is the common measure of five acute angles In mathematics, the trigonometric functions (also called circular functions, angle functions or goniometric functions) are real functions which relate an angle of a rightangled triangle to ratios of two side lengthsSin 2x formula is known as the double angle formula In this formula, we find the sine of the angle whose value is doubled We are familiar that sin is one of the primary trigonometric ratios that can be defined as the ratio of the length of the perpendicular to that of the length of the hypotenuse in a rightangled triangle
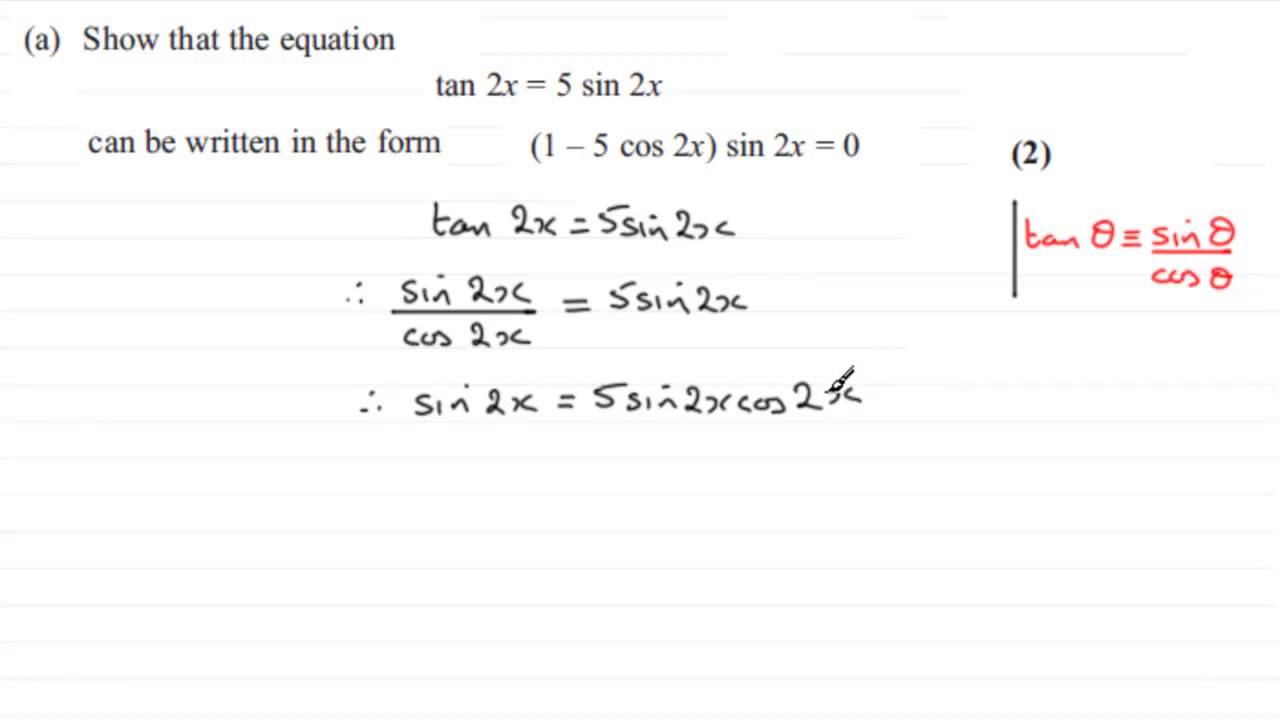



Edexcel Core Mathematics C2 June 12 Solutions Examples Worksheets Videos Activities
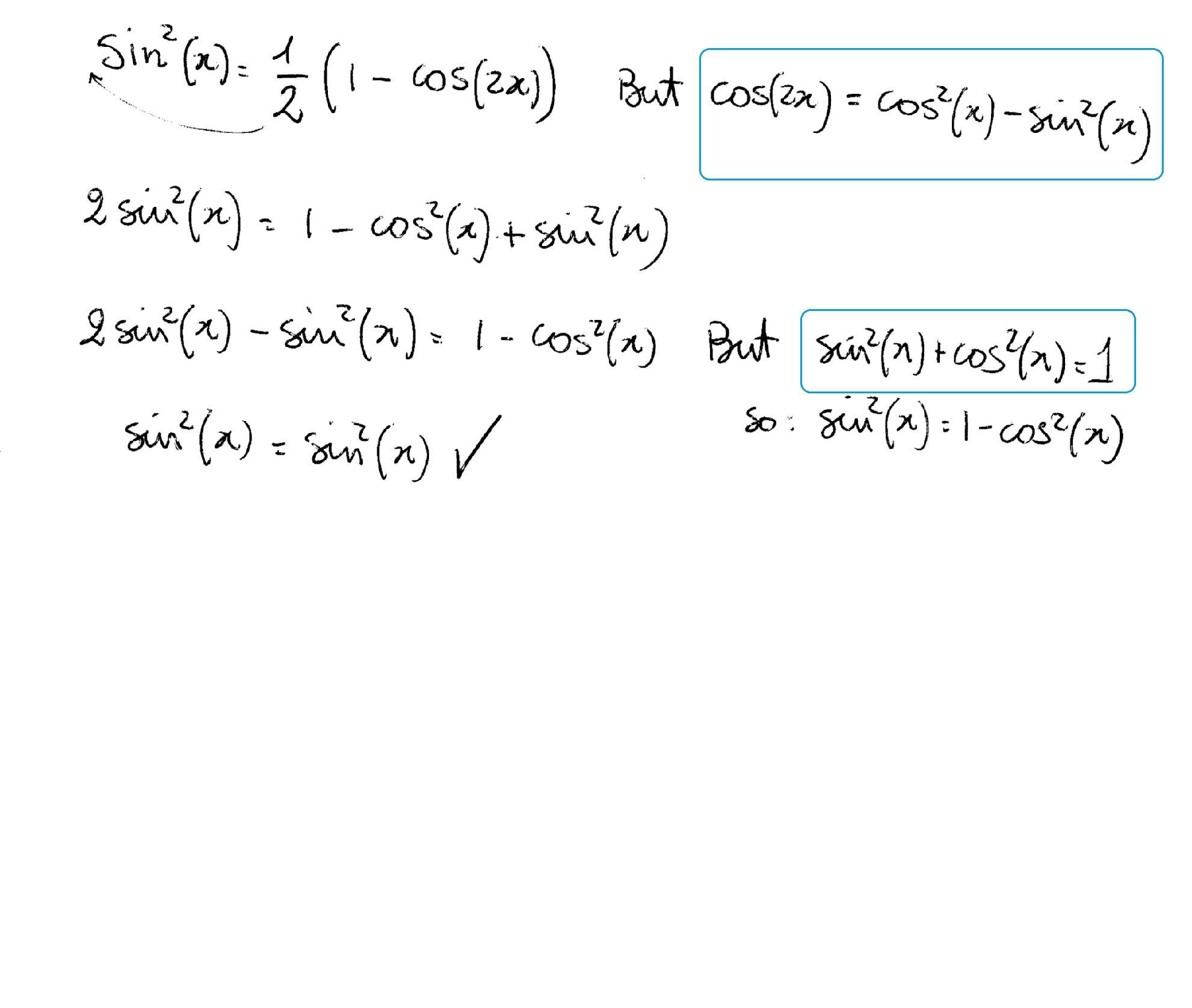



How Do You Verify Sin 2 X 1 2 1 Cos2x Socratic
Out of other 6 trigonometric formulas, let's have a look at the practice question of tan theta formula Example 1 If Sin x = 4/5, Find the value of Cos x and tan x?Formula sin 2 θ = 2 tan θ 1 tan 2 θ A trigonometric identity that expresses the expansion of sine of double angle function in terms of tan function is called the sine of double angle identity in tangent function\(\cos 2X = \frac{\cos ^{2}X – \sin ^{2}X}{\cos ^{2}X \sin ^{2}X} Since, cos ^{2}X \sin ^{2}X = 1 \) Dividing both numerator and denominator by \(\cos ^{2}\)X, we get \(\cos 2X = \frac{1\tan ^{2}X}{1\tan ^{2}X} Since, \tan X = \frac{\sin X}{\cos X} \)
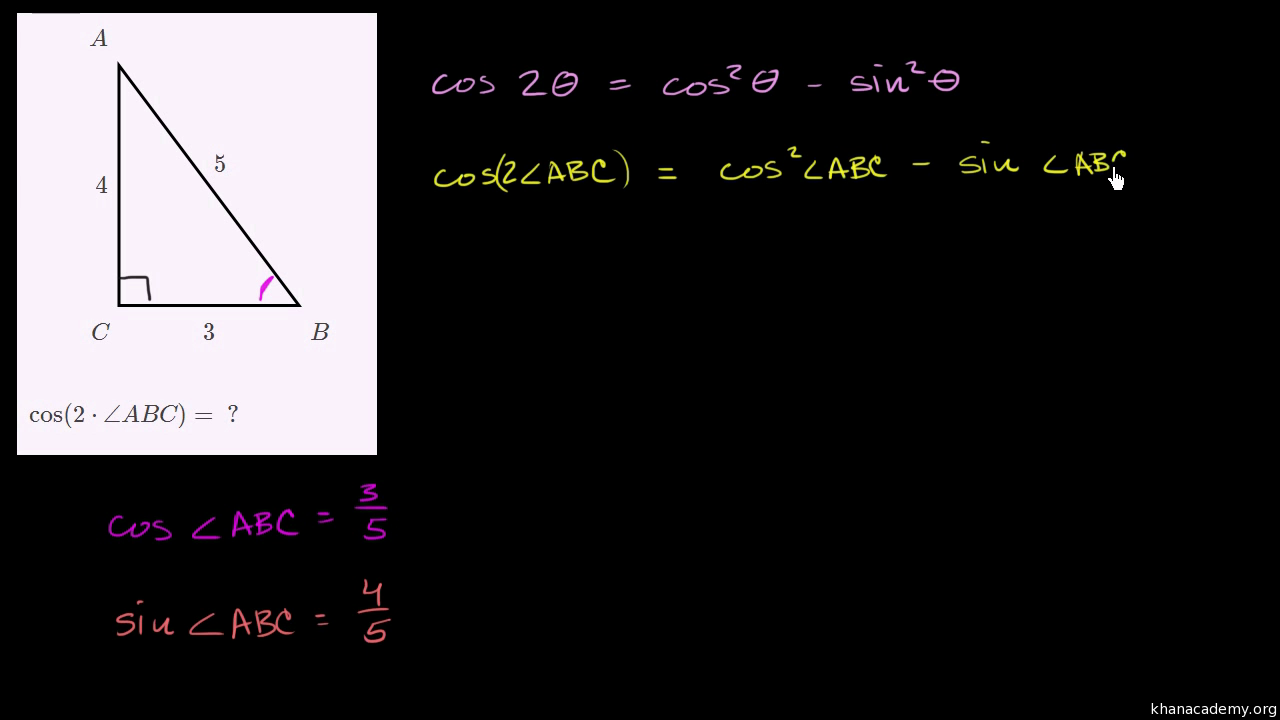



Double Angle Formulas Using Cosine Double Angle Identity Video Khan Academy




Section 7 3 Double Angle Half Angle And Sum
Cos 2x ≠ 2 cos x;One can show using simple geometry that t = tan (φ/2) The equation for the drawn line is y = (1 x)t The equation for the intersection of the line and circle is then a quadratic equation involving t The two solutions to this equation are (−1, 0) and (cos φ, sin φ) cos(ax)cos(bx) = 1 2cos((a − b)x) 1 2cos((a b)x) These formulas may be derived from the sumofangle formulas for sine and cosine Example 726 Evaluating ∫ sin(ax)cos(bx)dx Evaluate ∫sin(5x)cos(3x)dx Solution Apply the identity sin(5x)cos(3x) = 1 2sin(2x) 1 2sin(8x)




Sin2x Cos2x 1 Proof
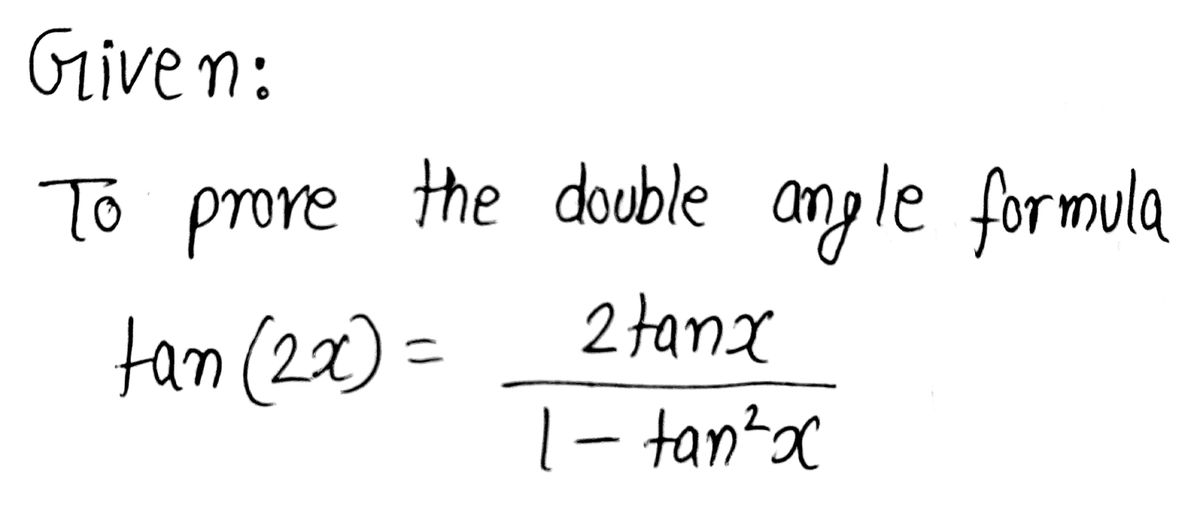



Answered Can You Guide Me Though The Proof Of Bartleby
2 tan1 x = sin1 (2x/(1x 2)), x ≤ 1 16 2tan1 x = cos1 ((1x 2)/(1x 2)), x ≥ 0 17 2tan1 x = tan1 (2x/(1x 2)), 1Formula to Calculate tan2x Tan2x Formula is also known as the double angle function of tangent Let's look into the double angle function of tangent ie, tan2x Formula is as shown below tan 2x = 2tan x / 1−tan2x where, tan x = Opposite Side / Adjacent Side tan 2x = Double angle function of tan x tan 2 x = Square funtion of tan xTan(2x) tan2x tan(2x) Identity for tan2x Proof of tan2x identity Formula for tan2x




Example 22 Solve Tan 2x Cot X Pi 3 Teachoo Examples




Trigonometry Reciprocal Identities Expii
2 x can be converted to 2 tan x 1 − tan 2 x using the double angle formula and the tan 2 x can be further be substituted to the following given item (tan Applying the 3 trig identities sin 2x = 2sin xcos x , and cos2x = (1 − 2sin2x) cosx = √1 − sin2x We get tan2x = 2sinxcosx 1 −2sin2x = = ( 2sinx 1 −2sin2x)√1 −sin2x Answer linkFormula 6Bolt, disc, quickrelease Spokes Stainless, 14g Tires Ground Control Sport, 29x23" Crankset Stout 2x, forged alloy Chainrings 22/36T Bottom Bracket Squaretapered, 73mm, internal bearings, 1225mm spindle Chain KMC X8 EPT, antirust coating, 8speed w/reusable Missing Link Front Derailleur Shimano Altus FDM315 Rear Derailleur
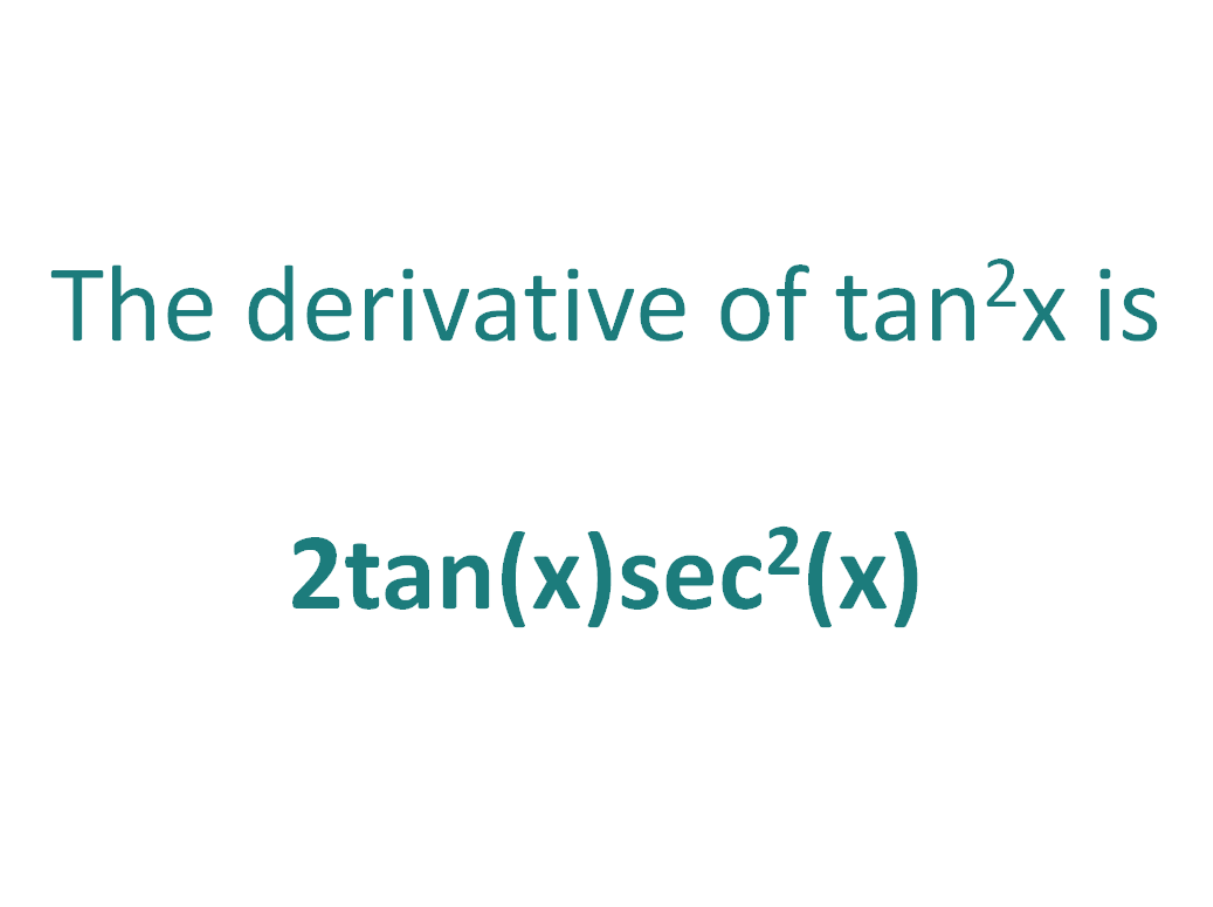



The Derivative Of Tan 2x Derivativeit



2
Double Angle formula to get 2sinxcosx Let's see what happens if we let B equal to A After doing so, the first of these formulae becomes sin (x x) = sin x cos x cos x sin x so that sin2x = 2 sin x cos x And this is how our first doubleangle formula,I know that and The next step would then be to say that but now what?Let cosx = Gand cos x lies below the x axis Find sin(2x),cos(2x) and tan(2x) b Proof the formula of unit circler y2 = 1, and explain it in your own wards (6 marks) (12 marks) 2 2 A boy is flying two kites at the same time He has (250m) feet of line out to one kite and (3m) feet to the other



Http Ougouag Com Trigreviewforcalc Pdf



Http Ougouag Com Trigreviewforcalc Pdf
Formula cos 2 θ = 1 − tan 2 θ 1 tan 2 θ A mathematical identity that expresses the expansion of cosine of double angle in terms of tan squared of angle is called the cosine of double angle identity in tangentThanks for the A!$\tan^2{x} \,=\, \sec^2{x}1$ $\tan^2{A} \,=\, \sec^2{A}1$ In this way, you can write the square of tangent function formula in terms of any angle in mathematics Proof Take, the theta is an angle of a right triangle, then the tangent and secant




Ex 3 3 23 Prove Tan 4x 4 Tan X 1 Tan2 X 1 6tan2x




Solve The Trigonometric Equation Tan X Tan 2x Tan X Tan 2x 1
Solve for x tan (2x)=1 tan (2x) = 1 tan ( 2 x) = 1 Take the inverse tangent of both sides of the equation to extract x x from inside the tangent 2x = arctan(1) 2 x = arctan ( 1) The exact value of arctan(1) arctan ( 1) is π 4 π 4 2x = π 4 2 x = π 4 Divide each term by 2Tan(x−y) = (tan x–tan y)/ (1tan x • tan y) Double Angle Identities sin(2x) = 2sin(x) • cos(x) = 2tan x/(1tan 2 x) cos(2x) = cos 2 (x)–sin 2 (x) = (1tan 2 x)/(1tan 2 x) cos(2x) = 2cos 2 (x)−1 = 1–2sin 2 (x) tan(2x) = 2tan(x)/ 1−tan 2 (x) sec (2x) = sec 2 x/(2sec 2 x) csc (2x) = (sec x csc x)/2; There's a very cool second proof of these formulas, using Sawyer's marvelous ideaAlso, there's an easy way to find functions of higher multiples 3A, 4A, and so on Tangent of a Double Angle To get the formula for tan 2A, you can either start with equation 50 and put B = A to get tan(A A), or use equation 59 for sin 2A / cos 2A and divide top and bottom by cos² A



2 Points Sprecalc7 7 3 029 16 Simplify The Chegg Com




Tan 2x Tan 2x
2x 3x formula Proving These formulas can be derived using x y formulas For sin 2x sin 2x = sin (x x) Using sin (x y) = sin x cos y cos x sin y = sin x cos x sin x cos x = 2 sin x




Calculus Formula Test Sheet Trigonometric Functions Function Mathematics




Inverse Trigonometric Functions General Solution Of Trigonometric Equations Pdf Dwrean Lhpsh




Tan2x Sin2x Tan2x Sin2x 5 1 Brainly In



2




1 Tan1 1 Tan2 1 Tan3 1 Tan45 2 N Brainly In Ryad Antonio Ebooks En Ligne Gratuit



Web Stanford Edu Class Archive Math Math Math 1144 Files Trig Pdf



How Do You Graph Y 4 Tan X Socratic




Ex 3 4 8 Find General Solution Of Sec 2 2x 1 Tan 2x Teachoo
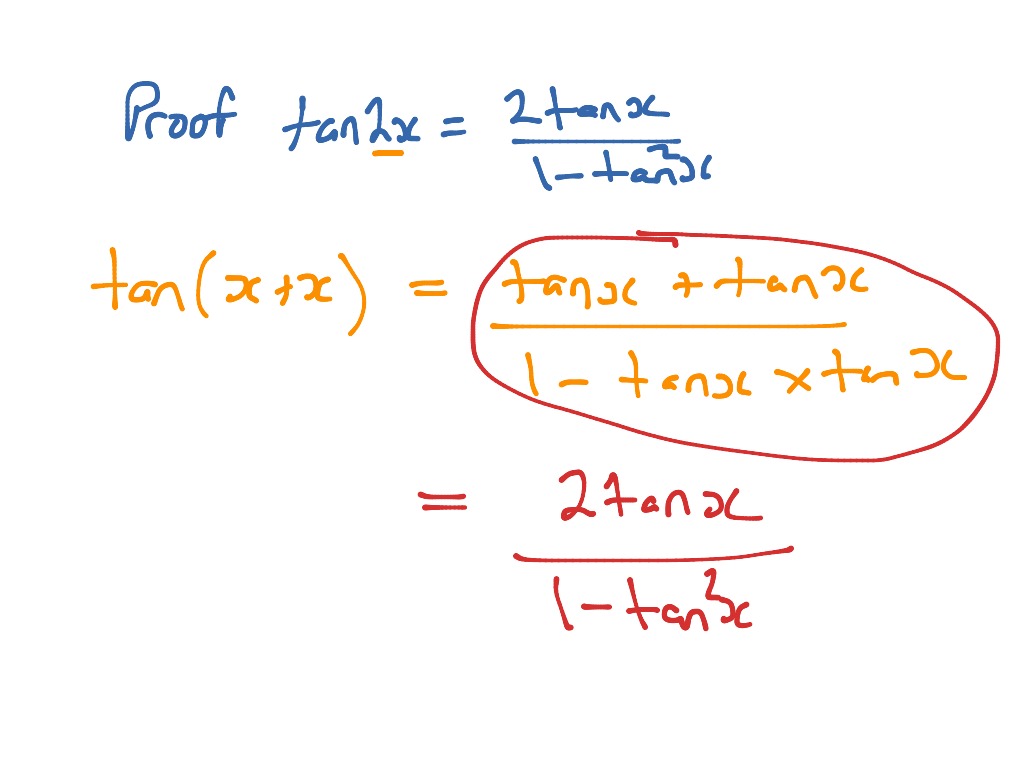



Treg Sam And Difference Formulas Math Algebra Trigonometry Proofs Showme




Ppt Trig 11 7 14 Powerpoint Presentation Free Download Id
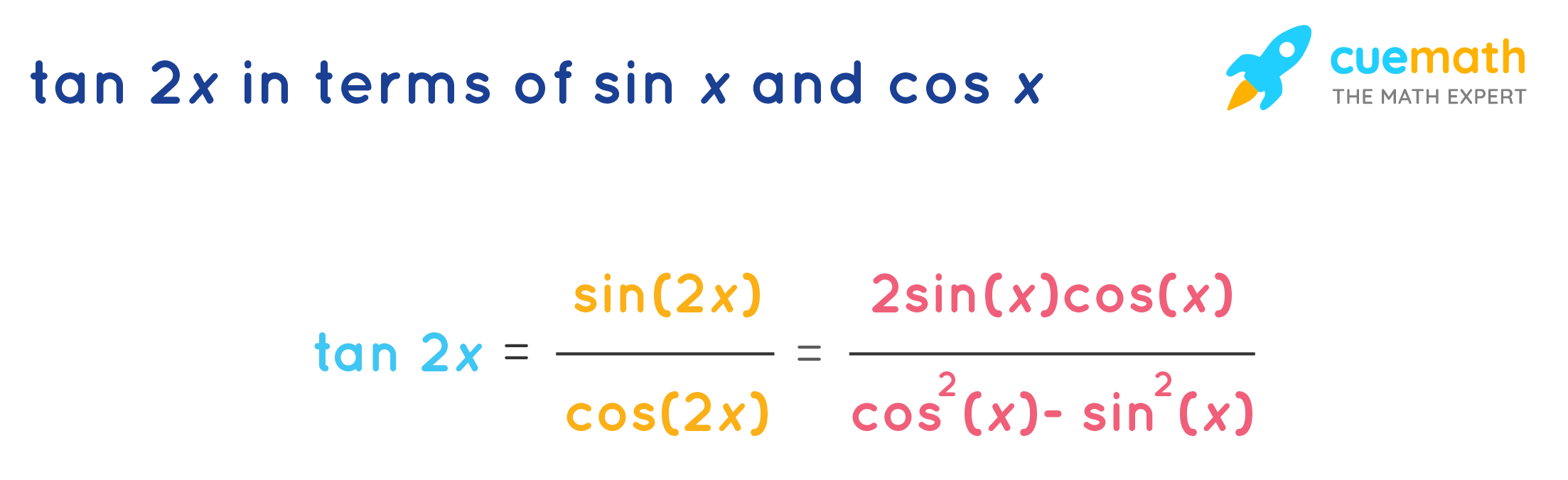



Tan 2x Formula What Is Tan 2x Formula Examples



Www3 Nd Edu Apilking Math Work Old exams Exams s13 M final sp13 solution Pdf




Trig Identity Sec2x Minus Tan2x T10 Youtube




How Many Can You Derive From First Principles Ppt Download



2




Half Angle Or Double Angle Examples Examples Solutions Videos Worksheets Games Activities



2




Examples Double Angle Formulas Ppt Download




Use A Sum Or Difference Formula To Write A Formula Gauthmath




Exam December 13 Questions Studocu




Prove That Tan 8x Tan 6x Tan 2x Tan 8x Tan 6x Tan 2x




人気ダウンロード Tan2 ただの悪魔の画像



1



Www Kpu Ca Sites Default Files Faculty of science 26 horticulture Mathematics Algtrig Studsol Ch9 Pdf



2




Quiz Worksheet Double Angle Formula Study Com



Www Jensenmath Ca Unit 5 pretest review solutions Pdf




Solution Solve For 8 In The Following Equation Sin 28 Cos8




Trigonometric Identities Trigonometric Functions Trigonometry
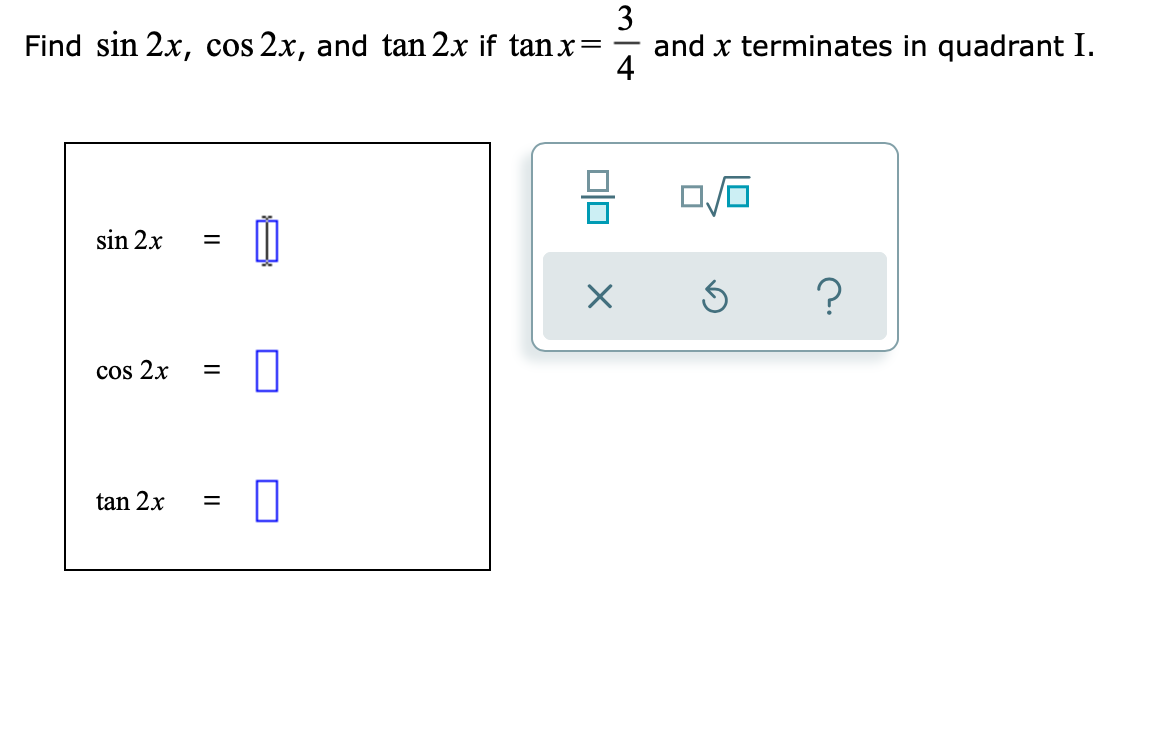



Answered 3 And X Terminates In Quadrant I 4 Bartleby



Knoxschools Instructure Com Files 7731 Download Download Frd 1 Verifier Nwvnfhcqjj3uwbxvthab5cvl9gai66hcxz8iywsc




If Tan 2 X Sec X A 0 Has Atleast One Solution Then Complete Set Of V Askiitians




Ex 3 4 8 Find General Solution Of Sec 2 2x 1 Tan 2x Teachoo




7 Questions On Differential Equations Exam 1 Math 1132 Docsity



Solved Dy Suppose 4 Sec2 2x Tan 2x Y 0 4 And Y 0 1 Da 2 A Find A Formula For Y A B Find A Formula For Y A Show And Explain Y Course Hero
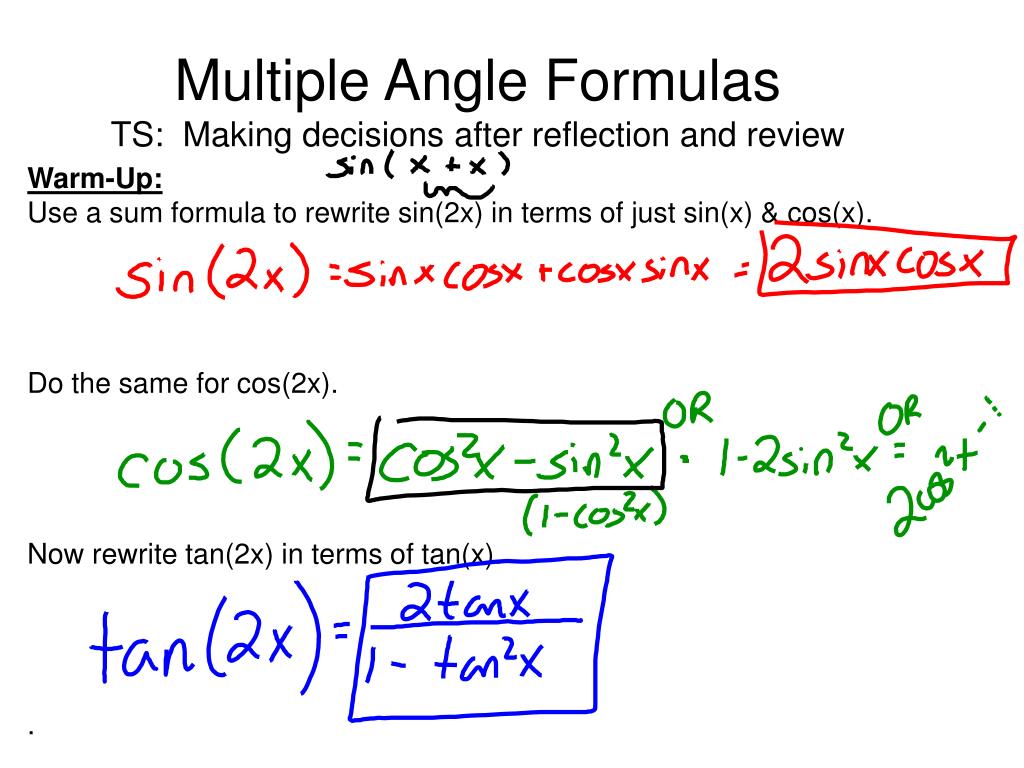



Ppt Multiple Angle Formulas Ts Making Decisions After Reflection And Review Powerpoint Presentation Id



Pure Math Formulas For Android Apk Download




Chapter 7 Trigonometry Flip Ebook Pages 1 14 Anyflip Anyflip




Section 7 3 Double Angle Half Angle And Chegg Com
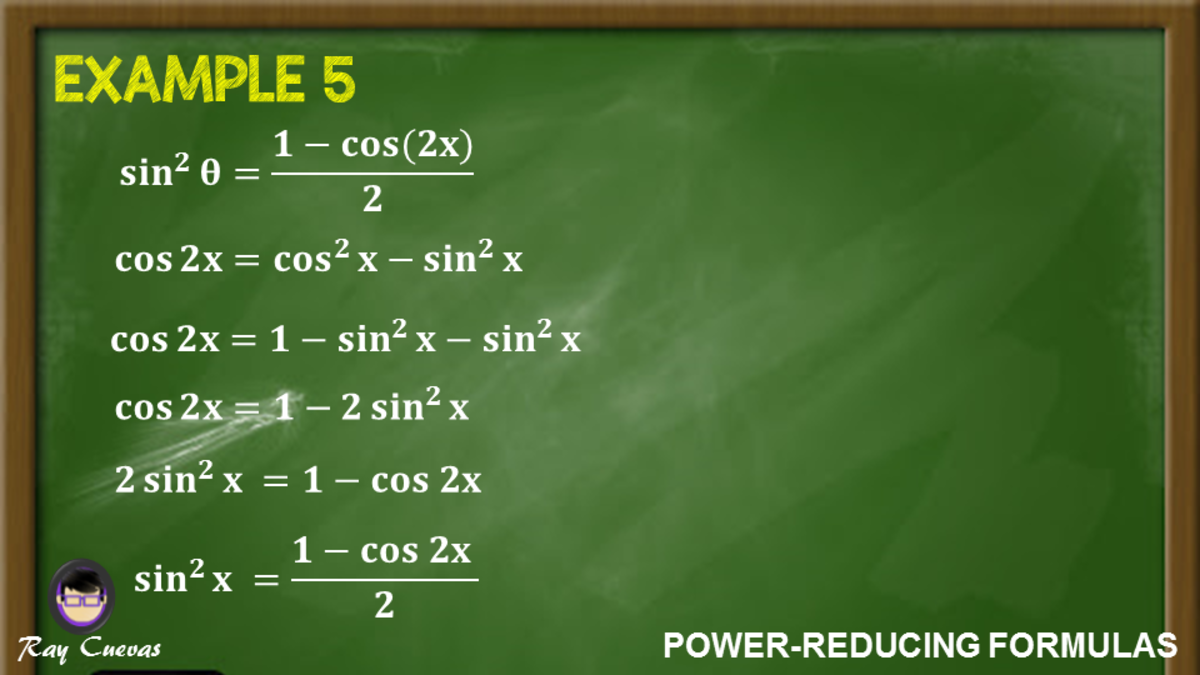



Power Reducing Formulas And How To Use Them With Examples Owlcation




Tan 2x Cot 2x 2 Youtube




Solve Tan2x Cot X Pi 3



2




How Do You Solve 1 Tan 2x 6 2sec 2x Socratic
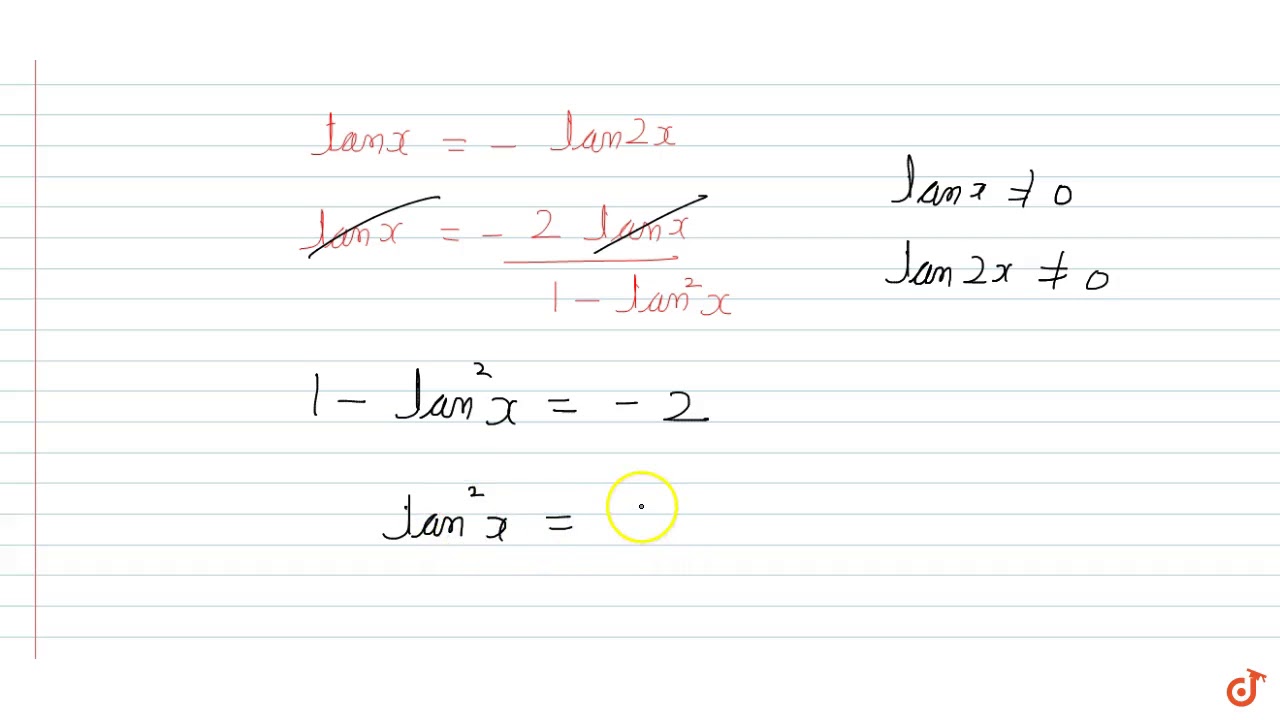



The General Solution Of The Equation Tanx Tan 2x Tan 2x Tanx 2 0 Is Youtube




Trigonometry Identities And Equations Ppt Download



2



Http Www Prestwick Sayr Sch Uk Uploads 1 0 7 2 Trig Past Papers Unit 2 Outcome 3 Answers Pdf




Double Angle Formulas What Are Double Angle Formulas Examples



2




Power Reducing Formulas And How To Use Them With Examples Owlcation



Www Thatonemathguy Com Uploads 7 0 1 3 Precalculus 2nd Edition Part 2 Pdf



3




Differentiate The Following From First Principle Tan 2x




Rd Sharma Solutions For Class 11 Chapter 5 Trigonometric Functions




Tan 2x Formula What Is Tan 2x Formula Examples
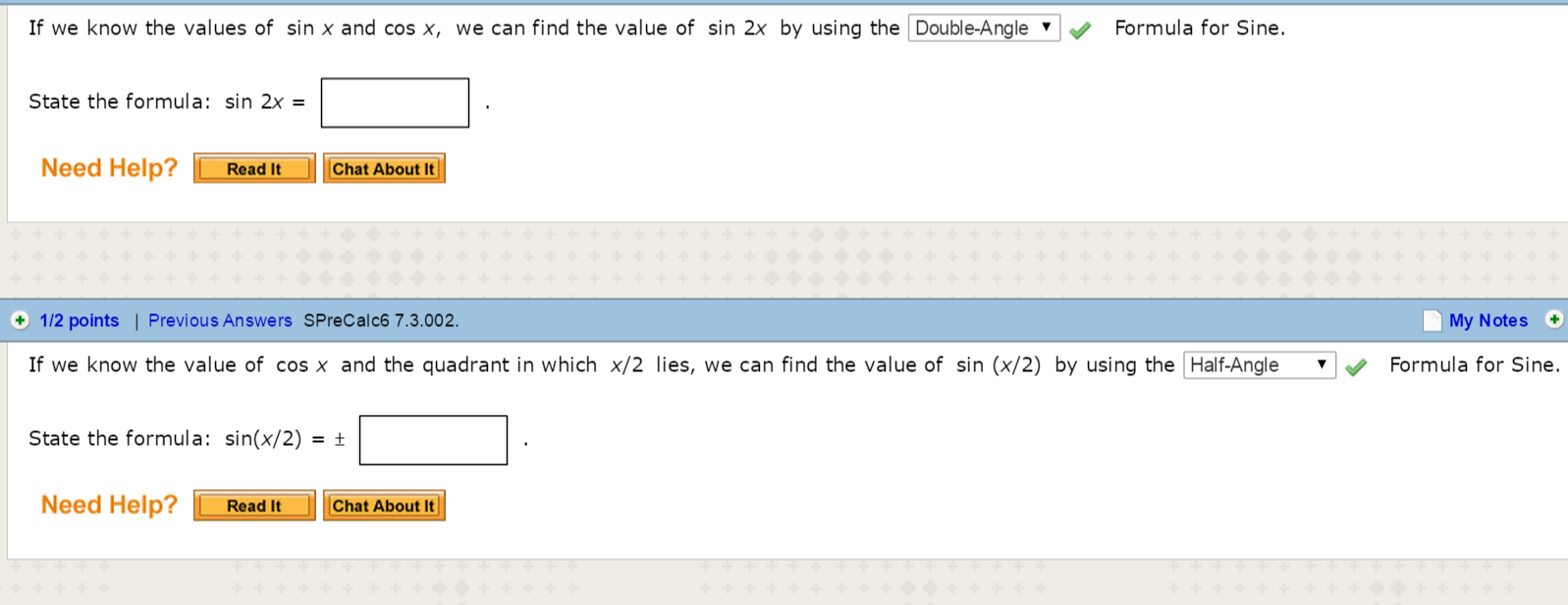



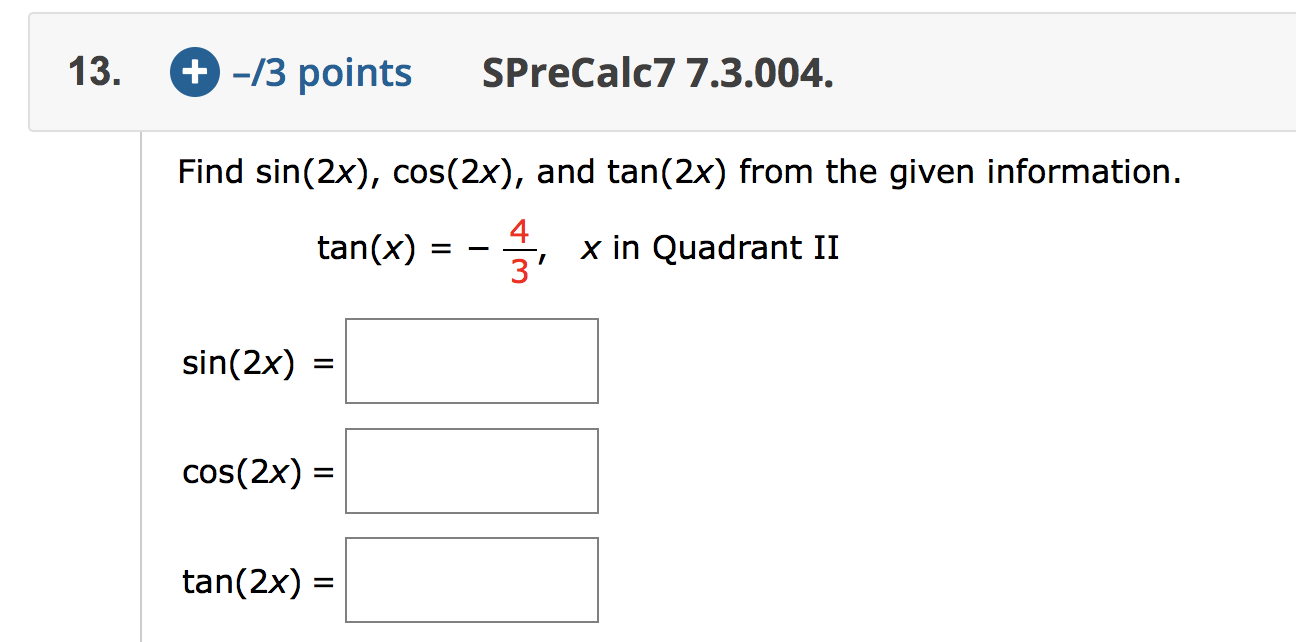
Find Sin 2x Cos 2x And Tan 2x From The Given Chegg Com




New Syllabus Additional Mathematics Pages 301 350 Flip Pdf Download Fliphtml5




Integration Calculus Notes



Yorkshiremathstutor Com Wp Content Uploads 19 02 8 Differentiation Answers Pdf



2



1



Solved 10 Points Salgtrig4 7 Write The Given Expression As An Algebraic Expression In X Cos 2 Tan1m E Find The Exact Value Of The Given Course Hero
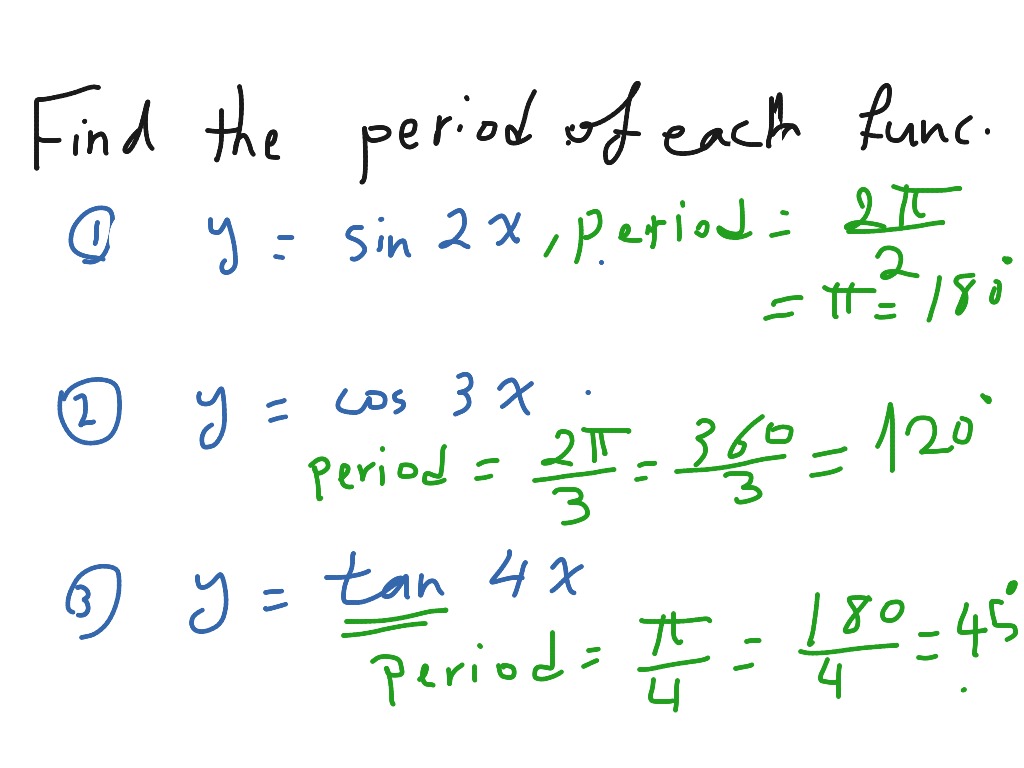



Find The Period Of Sin2x Cos 3x Tan 4 X Math Trigonometry Showme




Solution Solve For X In The Given Equation Arc Tan 2x Arctan X P




Trigonometry By Brandon Soto



2




Tan2x Tan 2x Identity For Tan2x Proof Of Tan2x Identity Formula For Tan2x Youtube




Integration Calculus Notes




The General Solution Of The Equation Tanx Tan2x Tanx Tan2x 1 Is Youtube




Cos 2x




Q 14 Show That Tan3x Tan2x Tanx Tan3x Tan2x Tanx Maths Trigonometric Functions Meritnation Com
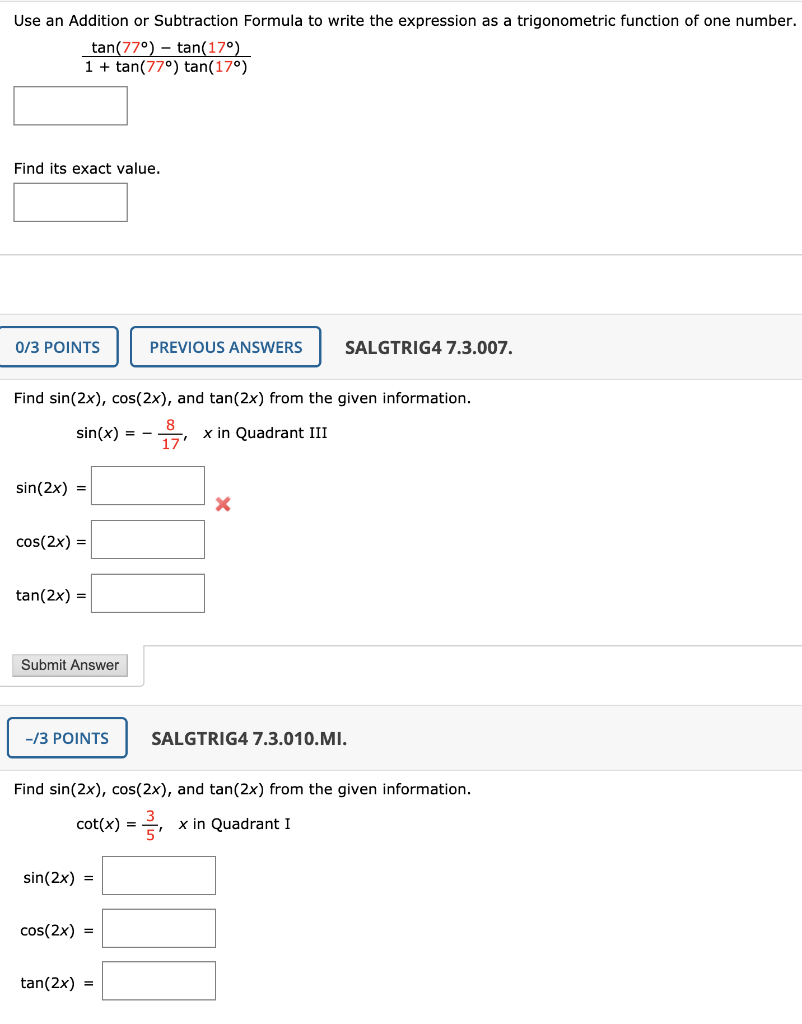



Use An Addition Or Subtraction Formula To Write The Chegg Com




Powers Of Trigonometric Functions



2



Http Www Math Brown Edu Tomg Formulas Pdf



Web Auburn Edu Holmerr 1617 Textbook Lhopital Print Pdf




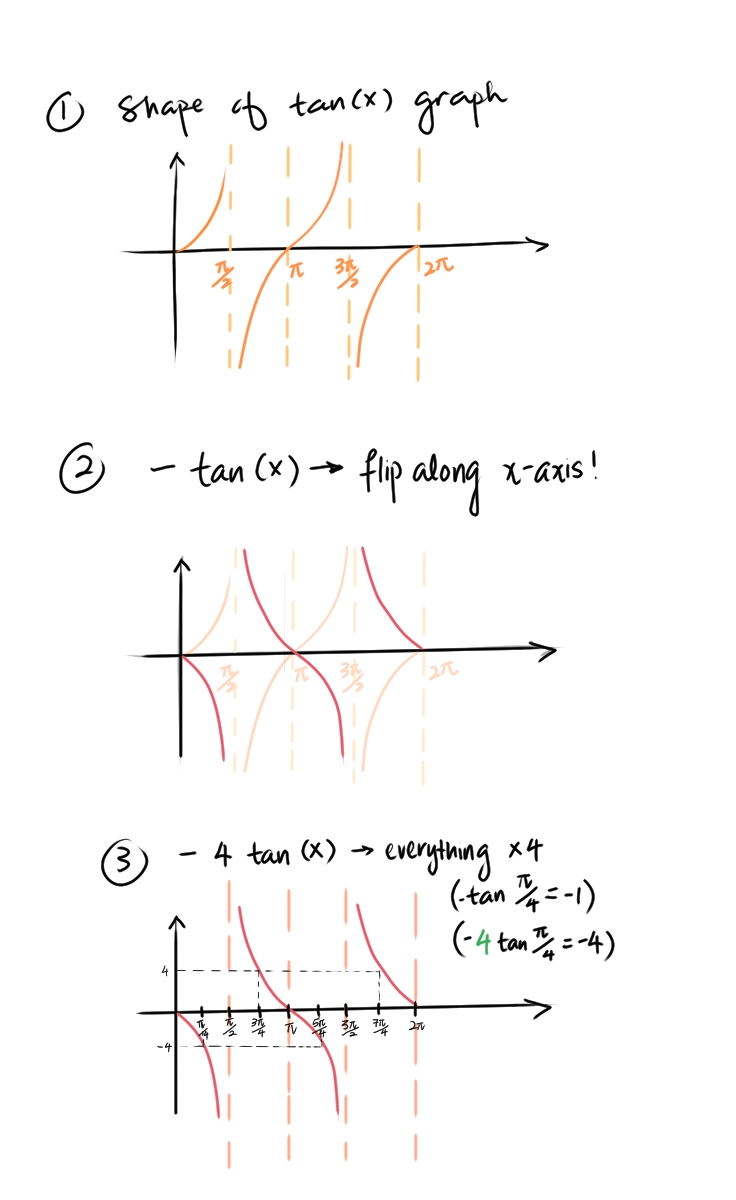
Howto How To Find Vertical Asymptotes Of Tan2x



0 件のコメント:
コメントを投稿